이번 글은 차원 축소의 대표적인 방법인 PCA와 FA에 대해 제가 교내 학회에서 강의했던 내용을 바탕으로 올립니다. 이 글의 수식은 연세대학교 응용통계학과 전용호 교수님의 ‘회귀분석’ 강의안의 수식을 참고하여 제 식으로 설명하기 쉽게 정리했음을 먼저 밝힙니다. 당시 강의 자료는 PDF를 참고하시면 됩니다. 오늘은 차원 축소의 대표적인 통계 기법인 PCA에 대해 알아보겠습니다.

1. Introduction

1.1. What is Dimension in data?

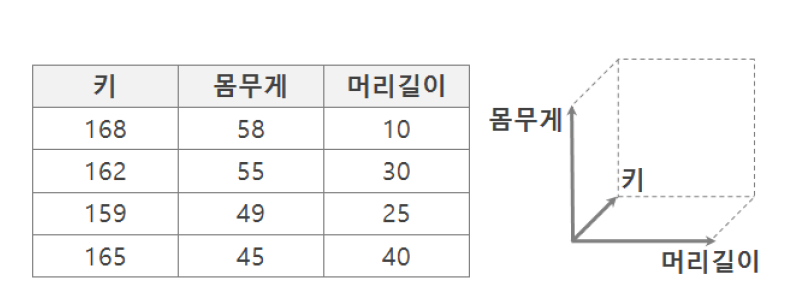
data in table

들어가기에 앞서서 데이터에서 차원이란 무엇일까요? 특히 테이블로 정형화된 데이터에서 생각해봅시다. 위와 같이 키, 몸무게, 머리 길이라는 변수가 있다면 간단히, 차원이란 변수의 개수라고 생각할 수 있습니다. 그러나 현실에서는 항상 변수들이 독립적(orthogonal)이지 않습니다. 예를들어 키와 몸무게는 강한 상관관계가 있다고 할 수 있죠.

1.2. The Curse of Dimensionality

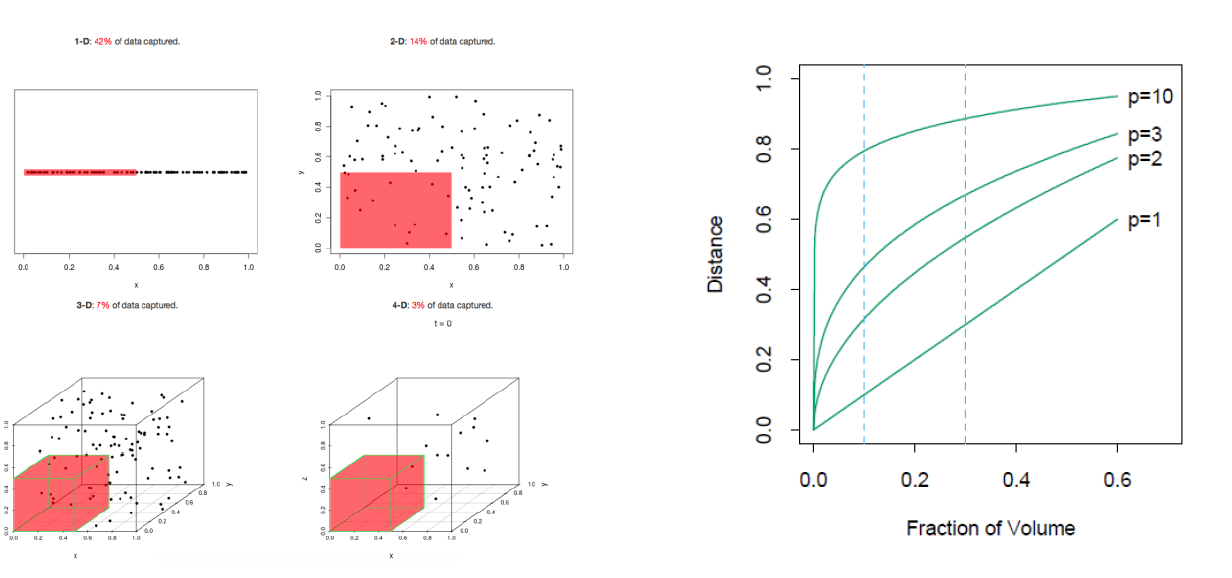
Machine Learning에서 feature가 하나 늘어나면 차원이 하나 증가합니다. 특히 Machine Learning에서 차원의 저주는 차원이 커질수록 역설적으로 성능 저하를 가져오는 것을 의미합니다. 왼쪽 그림을 보면 축의 0.5 거리에서 1차원에서는 데이터가 모여있지만 차원이 늘어날수록 점점 퍼지게 됩니다. 이렇듯 표본인 학습 데이터는 제한적임에 비해 차원이 계속 늘어난다면 학습 데이터가 그 공간을 충분히 설명하기 어렵습니다.

오른쪽 그림을 보면, 같은 공간을 설명하기 위해 필요한 차원의 수와 거리가 나타나있습니다. 1차원에서 10%의 공간을 채우기 위해서는 10%의 데이터가 필요합니다($0.1=0.1$). 그러나 10차원에서 10%의 공간을 설명하기 위해서는 각각의 축에 대해 80%의 데이터가 필요합니다($(0.8)^{10} = 0.1$). 즉, 공간은 기하급수적으로 증가하는 것에 비해 한정된 학습 데이터로 공간을 설명하기 때문에 과적합(overfitting)이 일어나고, 모델의 성능이 저하되는 것입니다. 이 뿐만 아니라 학습 속도도 상당히 느려집니다.

1.3. Dimension Reduction

따라서 차원의 저주 문제를 해결하기 위해 차원 축소가 필요합니다. 예를들어 MNIST 데이터셋이 있다고 할 때 이미지 한 장은 28*28=784차원의 데이터입니다. 이 데이터를 그대로 사용한다면 784차원을 모두 학습해야겠지만, 그렇다면 위에서 말한 문제가 발생할 수 있습니다.

img

따라서 모든 feature를 사용하는 것이 아니라 비슷한 픽셀 덩어리를 하나로 묶어서 보거나, 중요한 픽셀만 뽑을 수 있도록 하는 것이 차원 축소입니다. 즉, 고차원 데이터를 통째로 다 쓰는 것이 아니라 데이터를 압축하고 요약하여 큰 특징들만 사용하는 것입니다. 예를들어 획이 길쭉하거나, 획이 동그랗다는 2개의 큰 특징을 뽑을 수도 있습니다. 이는 Convolution layer를 사용하여 저차원의 feature map으로 주요 특징을 추출하는 것 또한 이미지의 차원 축소의 예라고 할 수 있습니다.

2. Principal Component Analysis(PCA)

2.1. Basic Idea of PCA

img

위의 그림을 운동장에 놀고 있는 아이들이라고 합시다. 만약 선생님이 최대한 한눈에 아이들을 보려면 어디서 봐야할까요? 왼쪽에서 보면 오른쪽에 있는 아이들이 가려져서 잘 보이지 않을 것입니다. 그러나 아래쪽에서 본다면 아이들이 최소한으로 가려지기 때문에 최대한 많이 볼 수 있습니다.

img

가로로 멀리 분산되어 있기 때문에 가장 많이 볼 수 있는것이죠! 즉, 퍼짐의 정도는 정보량에 비례합니다. 많은 정보를 담고 있는 소수의 새로운 축으로 데이터를 설명하는 것이 주성분분석(PCA)의 기본적 아이디어입니다.

2.2. What is PCA?

img

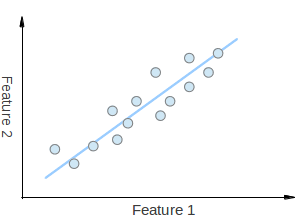
PCA는 최대 분산을 가지도록 기존 변수의 선형 결합을 찾습니다. 위처럼 Feature1과 Feature2를 조합하여 새로운 하늘색 축인 주성분(ex. PC = 0.5*Feature1 + 0.5*Feature2)으로 표현하는 것이죠.

아이디어

  • 몇 개의 작은 주성분이 원본 데이터에서 사용할 수 있는 거의 모든 정보를 포함할 수 있습니다.

목표

  • 데이터의 차원을 줄이고 실제 데이터의 차원을 발견합니다.
  • 의미 있는 새로운 변수를 발견합니다.

2.3. Linear Combination

위에서 말한 선형 결합에 대해서 잠깐 더 살펴보겠습니다. 변수가 $p$개, 관측치가 $n$개 의 변수가 있는 원 데이터 $\mathbf{X}$(p x n) 행렬이 평균을 중심(centered data)으로 되어있다고 가정합니다. 여기서 $x_{i}$는 데이터 행렬 $\mathbf{X}$의 행벡터(1 x n)입니다.

\[\mathbf{X} = \begin{pmatrix} x_{11} & x_{12} & \ldots \\ x_{21} & x_{22} & \ldots \\ \vdots & \vdots & \ddots \end{pmatrix} = \begin{pmatrix} x_{1} \\ x_{2} \\ \vdots \\ \end{pmatrix}\]

우선 이 $\mathbf{X}$ 가 아니라, $X_{i}$를 선형 조합한 새로운 $y_{i}$(1 x n)으로 표현하겠습니다.

\[\left\{\begin{matrix} y_{1} = a_{11}x_{1} + a_{12}x_{2} + \ldots + a_{1p}x_{p} = a_{1}^{T}\mathbf{X} \\ \vdots \\ y_{p} = a_{p1}x_{1} + a_{p2}x_{2} + \ldots + a_{pp}x_{p} = a_{p}^{T}\mathbf{X} \end{matrix} \right.\]

이러한 선형 결합은 $y_{i}$는 $\mathbf{X}$를 새로운 $a_{i}$(p x 1)의 축으로 사영(projection)한 것입니다. 만들어진 $y_{i}$로 구성된 행렬 $\mathbf{Y}$ (p x n)은 아래처럼 나타낼 수 있습니다.

\[\mathbf{Y} =\left( \begin{array}{cccc} y_{1} \\ y_{2} \\ \vdots \\ y_{p} \end{array} \right) =\left( \begin{array}{cccc} a_{1}^{T} \mathbf{X} \\ a_{2}^{T} \mathbf{X} \\ \vdots \\ a_{p}^{T} \mathbf{X} \end{array} \right) = A^{T} \mathbf{X}\]

2.4. PCA on Covariance

위에서 보았든 우리는 새로운 축으로 선형 결합된 $\mathbf{Y}$의 분산을 최대화하고 싶습니다.

\[Var(\mathbf{Y})=Var(A^{T}\mathbf{X})=A^{T}Cov(\mathbf{X})A\]

여기서 $a_{i}$의 norm은 1로 제약하고 분산을 가장 크게하는 $a_{i}$를 라그랑지안을 사용하여 구합니다.

\[\begin{aligned} \underset{a_{i}}{max}\{Var (\mathbf{Y})\} &= \underset{a_{i}}{max}\{ Var (a_{i} \mathbf{X}) \} \\ s&= \underset{a_{i}}{max} \{ a_{i}^{T} Cov (\mathbf{X}) a_{i} \} \end{aligned}\]

제약식을 $\lambda$ 안에 적어줍니다. \(L = a_{i}^{T}Cov(\mathbf{X})a_{i} - \lambda (a_{i}^{T}a_{i}-1)\) $a_{i}$로 미분한 식을 0으로 두고 최대값을 찾으면 아래와 같습니다.

\[\begin{aligned} \frac{\partial L}{\partial a_{i}} = Cov(\mathbf{X})a_{i} - \lambda a_{i} &= 0 \\ (Cov(\mathbf{X})-\lambda) a_{i} & = 0 \end{aligned}\]

고유벡터(eigenvector)의 정의에 의해 $a$는 $Cov(\mathbf{X})$의 고유벡터, 고유값(eigenvalue)의 정의에 의해 $\lambda$는 $Cov(\mathbf{X})$의 고유값이 됩니다. 즉 선형 조합의 계수 벡터인 $a_{i}$가 $\mathbf{X}$의 고유벡터(eigen vector)일 때 $Y_{i}$의 분산이 최대가 됩니다.

$Cov(\mathbf{X})$는 $XX^{T}$에 비례하며 이렇게 표현된 공분산은 Spectral Decomposition에 의해 아래처럼 분해됩니다.

\[\begin{gathered} \mathbf{XX^{T}} = \Sigma : \text{Covariance matrix (p x p)} \\ \text{By Spectral Decomposition, } \mathbf{XX^{T}} = \mathbf{VDV^{T}} \\ \text{where } \mathbf{V^{T}V}=\mathbf{VV^{T}}= \mathbf{I} \\ \text{with } \mathbf{V} \{ v_{1}, v_{2}, ..., v_{p} \} \text{ (eigenvectors)} \\ \text{ and }\mathbf{D}=diag \{\lambda_{1}, \lambda_{2}, \ldots \lambda_{p} \} \\ \text{with }\lambda_{1} \ge \lambda_{2} \ge \ldots \ge \lambda_{p} \ge 0. \text{ (eigenvalues)} \end{gathered}\]

따라서 $y_{i}$의 분산은 아래와 같이 쓸 수 있습니다.

\[\begin{aligned} Var(y_{i}) &= v_{i}^{T}Cov(\mathbf{X})v_{i} \\ &= v_{i}^{T}\mathbf{VDV^{T}}v_{i} \\ &=\lambda_{i} \end{aligned}\]

분산은 그에 대응한 고유값(eigen value)가 됩니다.

PCA3 \(\begin{aligned} max \big( var(Y_{i}) \big) &= \lambda_{i} \textrm{ : eigen value} \\ \textrm{when } a_{i} &= v_{i} \textrm{ : eigen vector} \end{aligned}\)

따라서 새로 만들어진 X의 선형 조합 $V^{T}X$는 주성분 축이 되며, 아래처럼 나타낼 수 있습니다. 가장 큰 고유값 순으로 그에 대응하는 고유벡터에 사영한 데이터들이 가장 큰 정보를 가지고 있습니다. 따라서 PC1, PC2, … 순으로 그 축이 데이터를 가장 많이 설명합니다. 또한 주성분 축은 선형 독립(orthogonal)한 고유벡터에 mapping하기 때문에 다중공선성(multicollinearity)을 해결합니다.

\[\begin{aligned} PC1 &= v_{1}^{T}X \\ PC2 &= v_{2}^{T}X \end{aligned}\]

위의 예시를 보면, 원 데이터를 0을 중심으로 이동한 뒤 고유벡터 2개로 이루어진 2개의 PC로 재구성된 것을 확인할 수 있습니다.

2.5. Result of PCA

주성분을 이용해서 표현하는 것은 소위 noise라 불리는 필요 없는 정보를 줄일 수 있습니다. 그러나 당연히 데이터의 정보를 잃어버리게 되겠죠. 그렇다면 몇개의 주성분을 사용해야 원래의 데이터를 얼만큼 설명할지 정해야합니다.

주성분의 수는 보통 Scree plot을 통해 정합니다. 통상적으로 고유값이 크게 꺽이는 ‘‘팔꿈치’‘부분에서 주성분의 개수를 정합니다. 아래의 경우는 주성분 3~4개 정도를 통상적으로 사용합니다.

sreeplot

주성분이 원래의 데이터에서 얼만큼을 설명하고 있는지는 고유값을 통해서 알 수 있습니다. 따라서 얼만큼 원 데이터를 잘 설명하고 있는지는 아래 고유값의 비율을 더한 누적 비율로 설명할 수 있습니다.

\[\frac{\lambda_{k}}{\sum^{p}_{i=1}\lambda_{i}}\]

PCA는 순차적으로 가장 큰 정보량을 먼저 담기 떄문에 가장 최소의 정보 손실을 보장할 수 있다는 장점이 있습니다. 그러나 이렇게 만들어진 PC는 원 변수의 조합이기 때문에, 그 변수를 해석해석하기 적절하지 않습니다.

3. Sparse PCA

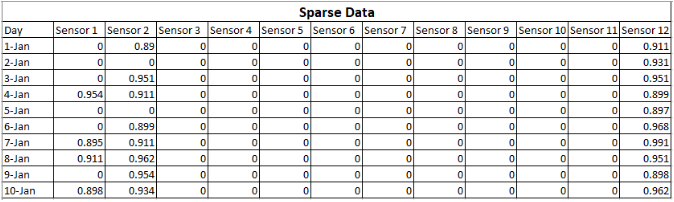
전통적인 PCA에 sparsity 제약 조건을 더하여 확장해준 개념의 Sparse PCA를 추가적으로 소개합니다. 차원이 매우 크면 PCA는 일관적이지 않고 해석하기에 어렵습니다. Sparse PCA는 특히 아래처럼 Sparse한 데이터에서 차원을 축소해주는 동시에 변수 선택을 동시에 할 수 있습니다.

sparsedata

Lasso, Ridge, Elastic net과 같은 방법들과 같이 L-norm과 $\alpha$를 수정하여 피팅합니다. 아래처럼 L1-norm이면 sparse한 변수들이 0으로 효과적으로 제거되어 변수 선택의 효과가 있습니다.

\[\begin{gathered} \min_{U, V}||X-UV||^{2}_2 + \alpha ||V||_{1} \\\\ \text{subject to } ||U_{k}||_{2} = 1 \text{ for all } 0 \le k < n \end{gathered}\]