0. 들어가며

Python을 이용한 알고리즘과 자료구조에 대해 공부한 내용을 바탕으로 간단히 포스팅할 계획입니다. 스파르타 코딩클럽의 알고보면 알기쉬운 알고리즘 강의를 수강하고 강의안을 참고하여 정리하였습니다.

알고리즘의 성능은 어떻게, 어떤 지표로 표현할 수 있을까요? 이번 포스트에서는 알고리즘의 복잡도와 이를 표기하는 빅오 표기법에 대해 살펴보도록 하겠습니다.

데이터마이닝 알고리즘 구현 과제에 교수님께서 학생들이 과도하게 루프문을 사용하는 것을 방지하는 차원에서, for문을 금지하신 적이 있었습니다. output이야 어떻게든 계산되어 출력하게 만들 수 있지만.. for문 없이 구현하려니 적잖이 애를 먹었습니다. 행렬 곱, map 등 갖은 방법을 동원해서 과제를 해결했었는데 컴퓨팅 타임을 비교하니 당연히 for문을 안 쓴 알고리즘이 훨씬 빠르고 깔끔했습니다. 그 때 효율적인 알고리즘에 대해 처음으로 깊게 고민했던 것 같습니다. 시간 복잡도를 통해서 루프문이 미치는 연산량의 차이에 대해 알아보겠습니다.

1. 시간 복잡도

시간 복잡도란?

알고리즘의 복잡도는 시간 복잡도와 공간 복잡도가 있습니다.

시간 복잡도란 input에서 output이 출력되는, 즉 문제를 해결하는 데 걸리는 시간과의 상관관계로 입력된 크기($N$)에 따라 실행되는 연산의 수로 나타냅니다. 입력값이 늘어났을 때 문제를 해결하는 데 걸리는 시간은 몇 배로 늘어나는지를 보는 것입니다. 당연히 입력값이 늘어나도 걸리는 시간이 덜 늘어나는 알고리즘이 좋은 알고리즘입니다.

공간 복잡도는 알고리즘이 실행될 때 사용하는 메모리의 양을 나타내는데, 요즘은 메모리의 발전으로 공간 복잡도의 중요도가 낮아졌습니다.

아래 array에 최대값을 찾는 예제를 통해 시간 복잡도를 구체적으로 살펴보겠습니다.

방법1.

input = [3, 5, 6, 1, 2, 4]

def find_max_num(array):
    for num in array:		# array의 길이(N)만큼 아래 연산이 실행
        for compare_num in array:		# array의 길이(N)만큼 아래 연산이 실행
            if num < compare_num:		# 비교 연산 1번 실행
                break
        else:
            return num

result = find_max_num(input)
print(result)

위에 연산된 것들을 더해보면, array의 길이를 N이라고 했을 때 $N(array의 길이) \times N(array의 길이) \times 1$ 의 시간이 필요합니다. 따라서 방법1의 시간 복잡도는

\[N \times N\]

입니다.

방법2.

input = [3, 5, 6, 1, 2, 4]

def find_max_num(array):
    max_num = array[0]		# 연산 1번 실행
    for num in array:		# array의 길이(N)만큼 아래 연산이 실행
        if num > max_num:		# 비교 연산 1번 실행
            max_num = num		# 대입 연산 1번 실행
    return max_num

result = find_max_num(input)
print(result)

위에 연산된 것들을 더해보면, array의 길이를 N이라고 했을 때 $ 1 + N(array의 길이) \times (비교 연산 1번 + 대입 연산 1번) $ 의 시간이 필요합니다. 따라서 방법2의 시간 복잡도는

\[1 + 2 \times N\]

입니다.

방법1. vs. 방법2.

두 방법의 시간 복잡도를 비교해보겠습니다.

$N$의 크기 방법1. $N^2$ 방법2. $2N+1$
1 1 3
10 100 21
100 10000 201
1000 1000000 2001
10000 100000000 20001

N의 크기가 커질 수록 $N^2$의 숫자가 훨씬 더 큰 차이를 보입니다. 또한 $2N+1$에 상수는 미미한 숫자 차이이므로 무시할만 한 정도이므로 $2N+1$의 연산량은 가장 큰 영향을 미치는 N의 텀인 $2N$만 보면 됩니다.

2. 점근 표기법

점근 표기법(asymptotic notation)은 어떤 함수의 증가 양상을 다른 함수와의 비교로 표현하는 수론과 해석학의 방법으로, 알고리즘의 성능을 수학적으로 표기하는 방법으로 쓰입니다.

  • 빅오(Big-O) 표기법은 최악의 성능이 나올 때 어느 정도의 연산량이 걸릴것인지에 대해 표기합니다.
  • 빅오메가(Big-Ω) 표기법은 최선의 성능이 나올 때 어느 정도의 연산량이 걸릴것인지에 대해 표기합니다.

예시를 들어 살펴보겠습니다. 배열을 돌면서 배열의 원소가 찾고자하는 숫자와 같은지 비교하는 아래 알고리즘이 있습니다.

input = [3, 5, 6, 1, 2, 4]

def is_number_exist(number, array):
    for element in array:		# array의 길이(N)만큼 아래 연산이 실행
        if number == element:		# 비교 연산 1번 실행
            return True
    return False

result = is_number_exist(3, input)
print(result)

위에서 연산된 것들을 더해보면, 총 $ N \times 1 $의 시간 복잡도를 가집니다. 그런데 여기서 모든 경우에 $N$ 만큼의 시간이 걸릴까요?

만약 3과 같은 숫자를 찾고 있다면 1번만에 찾을 것이고, 4를 찾는다면 6번만에 찾을 것입니다. 최선의 성능일 때의 연산량은 1, 최악의 성능일 때의 연산량은 6입니다.

따라서 빅오 표기법으로 $O(N)$, 빅오메가 표기법으로 표시하면 $\Omega (1)$ 의 시간 복잡도를 가지고 있습니다.

이처럼 알고리즘의 성능은 항상 동일한 게 아니라 입력값에 따라 달라질 수 있습니다. 그러나 알고리즘에서는 빅오 표기법으로 분석합니다. 왜냐면 대부분 최악의 경우에 시간이 얼마나 소요될지를 대비해야하기 때문입니다.

앞서 최대값을 구하는 알고리즘 방법1과 방법2의 시간복잡도는 Big-O 표기법으로 아래처럼 나타낼 수 있습니다.

구분 방법1. 방법2.
시간 복잡도 $N^2$ $2N+1$
Big-O 표기법 $O(N^2)$ $O(N)$

시간 복잡도 그래프

빅오 복잡도는 대표적으로 아래 그래프와 같은 관계를 가집니다.

참고: https://www.bigocheatsheet.com


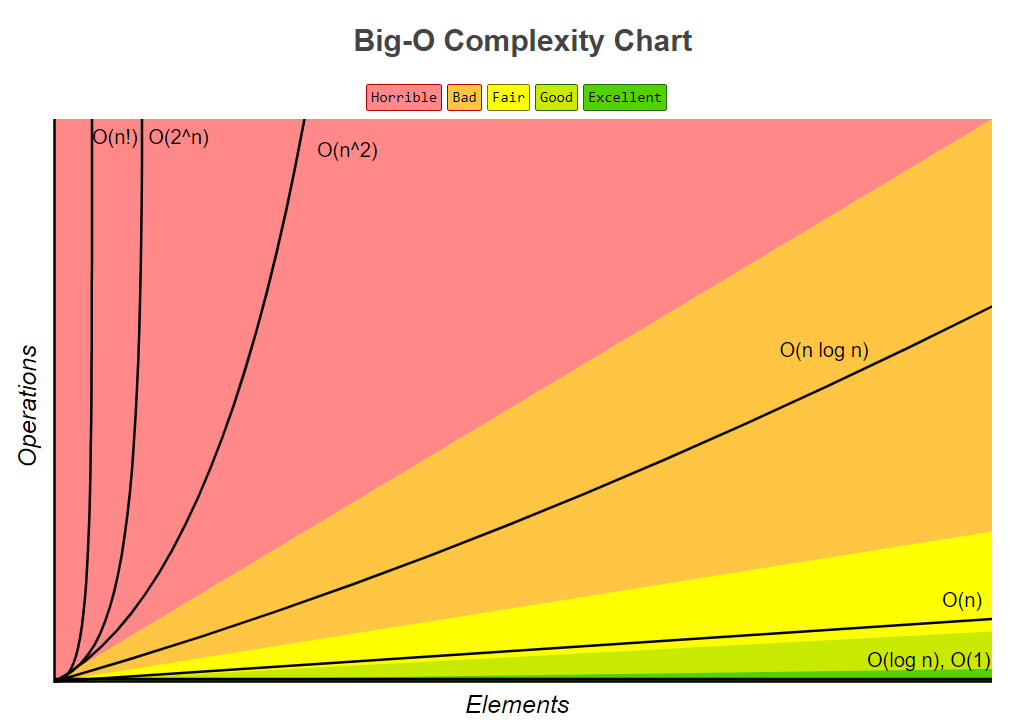
N이 커질수록 엄청나게 큰 연산량의 차이가 생깁니다. $O(N^2)$와 $O(N)$의 엄청난 차이도 확인할 수 있습니다.

효율적인 알고리즘을 어떻게 측정하는지에 대해서 살펴보았습니다. 단순히 ‘다중루프가 연산량이 많다’ 라고는 알았지만 직접 연산량을 구하고 빅오 표기법으로 계산해보니 어떻게 구현하는 알고리즘이 효율적인 알고리즘인지 확 느껴지네요.

알고리즘의 복잡도는 루프문 뿐만 아니라 정렬과 자료구조에서도 차이를 보이니 자세한 내용은 참고 사이트에서 확인하시면 될 것 같습니다.

Reference