Samsung AI Forum 2022(SAIF 2022)에서 열린 Yoshua Bengio 교수의 Keynote Speech인 ‘분할 베이지안 인과 모델이 필요한 이유(Why we need amortized causal and Bayesian World models)’를 듣고 우리말로 설명을 정리하였습니다.

Yoshua Bengio - Keynote Speech

11월 8일 Day 1의 Keynote Speech는 AI의 캐나다 몬트리올 대학교의 컴퓨터학 교수 Yoshua Bengio가 맡았습니다. Bengio 교수는 딥러닝의 창시자로 컴퓨터계의 노벨상이라 불리는 튜링상을 수상한 세계적인 거장입니다. 제프리 힌튼, 얀 르쿤, 앤드류 응과 함께 AI 4대 천왕으로 꼽히기도 합니다. Bengio 교수는 2020년에 삼성 AI 교수로 임명되었으며 삼성종합기술원(SAIT)의 공동연구원으로 오랜 동안 함께 연구를 해왔다고 합니다.

Bengio 교수는 ‘분할 베이지안 인과 모델이 필요한 이유’를 주제로 기조 강연을 하였습니다. 과학 분야에서 이론을 탐색하거나 실험을 설계하는 AI와 일반적인 AI를 위한 인과 모델에 적용한 분할 추론(Amortized causal)과 베이지안(Bayesian) 방법을 설명하고 이를 활용한 최신 연구 성과에 대해 공유하였습니다. Bengio 교수는 신 재료를 발견하는 머신러닝 연구 중, 이 연구를 더 폭 넓게 다른 과학적 발견이나 강화학습, 과학적 모델링 등에 적용할 수 있다는 걸 발견하여 연구했다고 합니다.

참고로 이 강연 내용은 기본적으로 베이지안이 무엇인지에 대한 이해가 선행으로 필요합니다. 그럼 강연 내용을 우리말로 풀어 설명해보겠습니다.

분할 베이지안 인과 모델이 필요한 이유 (Why we need amortized causal and Bayesian World models)

Bengio 교수는 오늘 머신러닝 컨퍼런스에서 통상적으로 들을 수 있는 연구 방향과 다른 주제를 얘기할 것이라 하며 시작합니다. Bengio 교수가 최근 몇 년간 던진 질문인 ‘Out of distribution generalization’(OOD)이라 불리는 머신러닝의 한계가 있습니다. 머신러닝의 고전적 관행과 learning theory는 한 분포에서 학습한 모델을 동일한 분포에 적용하는데, 불행히도 현실세계는 그렇지 않다는 것입니다. 상황이 변하거나 다른 분포에 적용하는 경우가 있기 때문이죠. 그러면 성능이 떨어지게 됩니다.

이것은 매우 실제적인 문제인데, 이것은 이미 학습된 머신러닝이 새로운 상황과 새로운 과제에 적응하기 위해 얼마나 많은 예시가 필요한지에 대한 문제로 연결됩니다. 사람(human)과 기계 혹은 컴퓨터(machine)는 정말 다릅니다. 사람은 경험과 언어를 통해서도 배울 수 있습니다. 그러나 머신러닝은 지식을 모듈화하고 재사용하는데에 추론 능력이 낮으며, 낮은 수준의 데이터를 이용해서 학습한다는 한계가 있습니다.

OOD 문제를 더 잘 이해하기 위해 예시를 들었습니다. 사람은 훈련 데이터와 같지 않은 분포에서도 일반화할 수 있다는 점에 대해 생각해 보겠습니다. 만약 당신이 한번도 가보지 않은 달에 간다면 어떨까요? 우리는 달의 환경을 바로 이해할 수 있겠죠. 지구와 똑같은 물리학이 작용하기 때문입니다. 대기와 중력과 같은 컨디션만 다를 뿐입니다.

이와 마찬가지로 관찰 데이터가 훈련 데이터와 다른 분포를 보여도, 인과 법칙(causal mechanism)을 공유하고 있습니다. 따라서 우리가 훈련하는 데이터의 분포 바깥의 다른 분포에도 공유되는 동일한 인과 법칙을 일반화 할 수 있습니다. 이것이 바로 인과 모델의 아이디어 입니다.

인과 모델(Causal model)은 다른 하나의 분포가 아니라 분포 집단(family of distribution)을 따르고 있습니다. 그리고 하나의 분포가 다른 분포와 다른 점은 개입(intervention), 환경(environment), 초기 상태(initial state)라 불리는 파라메터가 다르다는 것입니다. 이 파라메터는 모든 분포에 공유하고 있으며, 인과 법칙이라고 부르는 것이 작동하는 것을 설명합니다. 개입이란 예를 들어서 사람이 문을 열어 방의 온도가 따뜻해지는 결과를 가져오는 추상적인 행동같은 것입니다. 이 행동으로 많은 분포가 달라질 수 있겠죠.

우리가 개입이 다른 분포에서 나온 데이터를 볼 때, 우리는 우리가 한번도 보지 못했지만 같은 분포 집단(family of distribution)에 있는 분포로 일반화할 수 있습니다. 이것이 인과 기계 학습의 전제입니다. 자 그럼 여기까지 우리가 OOD 문제에 이런 종류의 결과를 얻기 위해 인과 법칙이 왜 필요한지 설명했습니다.

아시다시피 이 강연 제목의 큰 단어는 Bayesian입니다. 베이지안 기계 학습의 아이디어는 머신러닝 초기에 통계와 베이즈 정리로부터 존재했지만, 실제로 산업 분야의 최첨단 머신러닝을 따라잡지 못했습니다. 자 그럼 우리가 왜 베이지안 접근법을 원하는지와 그것이 무슨 의미인지 먼저 살펴봅시다.

당신이 데이터를 살펴보면, 여러 이론과 모델과 여러 다른 파라미터를 가진 여러 신경망이 있을 겁니다. 그리고 당신은 어떤 것이 맞는 이론인지, 맞는 모델인지 고르기에 충분한 정보를 주지 않는 한정된 크기의 데이터를 가지고 있을 겁니다. 머신러닝의 기본적인 방법은 무작위로 그 중에 하나를 선택하고, 그 데이터가 맞는 모든 모델을 좋은 모델로 꼽습니다. 그러나 데이터에 잘 맞는 모델이 여러개 있다면 이는 잘못된 것일 수 있습니다. 따라서 베이지안 머신러닝의 아이디어는 데이터에 호환되는 모든 모델과 이론에 대해 추적을 시도해봅니다.

실제로 이것은 꽤 어려울 것 같죠? 왜냐면 아마 엄청 무한한 경우의 수가 있을 수 있기 때문이죠. 그리고 베이지안 계산은 아시다시피 다루기 힘든 계산을 요구하기 때문입니다. 따라서 과거에는 연구자들은 베이지안 사후분포(posterior)라 불리는 family of model의 근사를 제안했습니다. 그러나 불행히도 이러한 근사는 비현실적인 경향이 있습니다. 예를 들어 모든 것이 선형이라는 가정을 하면 정확한 베이지안 계산을 할 수 있지만, 이것은 너무 강한 가정입니다.

그러나 우리는 이제 실제로 이 것을 다룰 수 있는 딥러닝 수준에 도달했습니다. 딥러닝은 아주 복잡한 분포를 큰 신경망과 큰 데이터셋으로 학습할 수 있습니다. 따라서 당신은 제가 어떤 말을 하려는지 알텐데요, 딥러닝의 기술이 정확하고 풍부한 베이지안 사후분포를 학습하는데 쓰일 수 있습니다.

당신이 만약 자율주행을 위한 머신러닝 시스템을 만든다면, 당신은 이것이 확신있게 잘못된 결정을 하는 것을 원하지 않을 것입니다. 신경망의 초기 가중치 같은 것에 좌우되기 때문에 옳은 이론과 잘못된 이론이 있다면 이 둘 중에 어떤 것이 선택될지 알 수 없습니다. 만약 ‘사고가 나는’ 잘못된 이론을 취한다면 그 결과는 치명적입니다. 따라서 우리가 베이지안이 아니라면, 안전 상의 위험과 틀릴 수도 있는 일을 맞게 한다고 확신을 가지고 하는 시스템의 리스크가 있습니다.

분할(Amortization)의 뜻은, 내가 어떤 상황에서 ‘왼쪽으로 가야할지, 오른쪽으로 가야할지’ 질문을 던질 때에 Monte Carlo Markov Chain(MCMC)와 같은 비싼 연산을 하지 않는 대신에 신경망을 학습시켜서 미리 계산하는 것입니다. 따라서 신경망을 훈련하며 비용을 지불하지만 그러나 런타임에 바로 대답을 얻을 수 있습니다. 그렇지 않으면 MCMC 접근 방식은 꽤 비싼데 이것은 훨씬 기초적이라는 데에서 계산상 이점이 있습니다.

좋은 이론의 수와 사후 분포의 형태의 수는 기하급수적으로 커질 수 있는데, 이를 고려하기 위해 모든 것을 방문해야하는 것은 실용적이지 않습니다. 그러나 이것은 머신러닝이 완전히 해결할 수 있는 부분입니다! 머신러닝은 일반화에 대한 것입니다. 일반화란 어떤 분포에서 나온 적은 수의 예시에서 모든 다른 분포에 합리적으로 일반화하는 것입니다.

데이터에 호환되는 모든 이론을 생각해보겠습니다. 당신이 가진 모델로 어떻게 다른 이론이 데이터에 맞는지 정보를 얻을 수 있다면 신경망은 패턴을 찾고, 모든 다른 이론에 일반화할 수 있습니다. 왜냐하면 구조가 있기 때문이죠. 이것은 머신러닝을 사용하여 데이터 안에 포착할 수 있는 구조가 항상 있습니다. 만약 데이터 안에 구조가 없다면, 머신러닝은 쓸모가 없습니다. 그리고 또 사람의 뇌 또한 쓸모가 없습니다. 왜냐면 우리 주변의 세상은 우리가 이해할 수 있는 구조로 가득차있기 때문입니다.

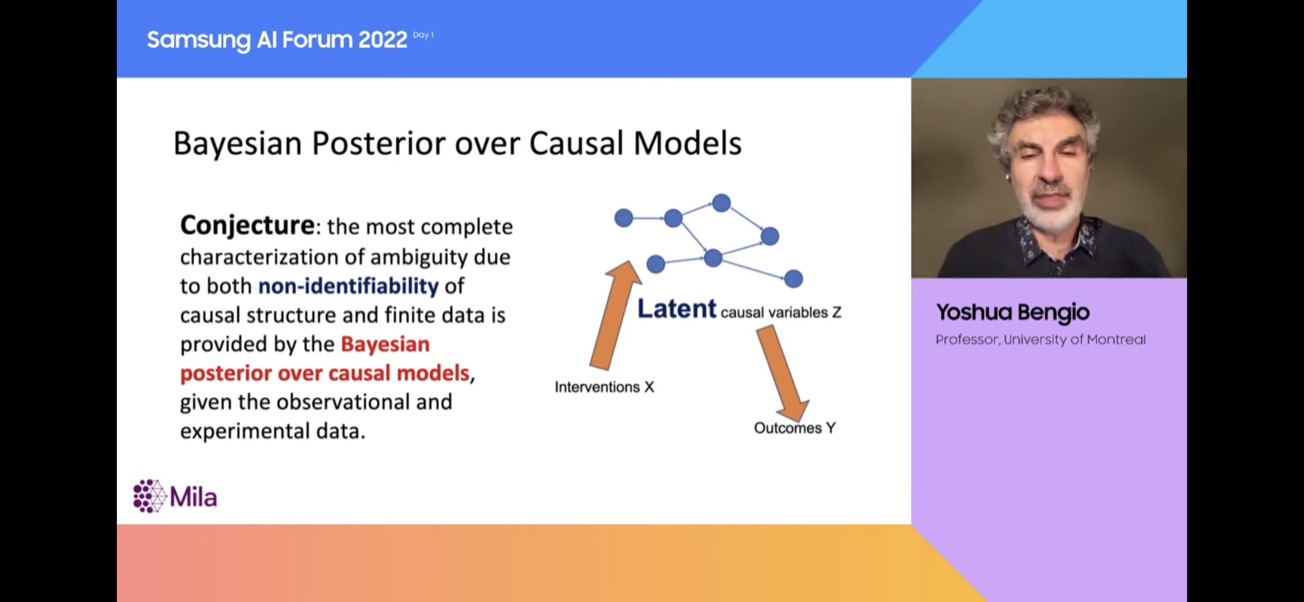
아주 많은 데이터가 있어도, 간섭(intervention)이 하나 없는 기본 환경에서의 데이터만 있다면, 당신은 다른 개입(intervetion)이 있는 다양한 실험을 해야할 것입니다. 만약 우리가 관심있는 인과 변수의 관찰조차 하지 못한다면, 상황은 더 어렵겠죠. 실제 상황에서는 문제가 많습니다.

그러나 인과 모형을 찾는 베이지안 방법은 이성적인 방법입니다. 이것은 우리에게 데이터에 호환되는 모든 이론에 대해 알려줄 수 있습니다. 이것이 ‘베이지안’과 ‘인과’에 흥미로운 연관성입니다.

  • 영상 링크 - [SAIF 2022] Day 1: Keynote (Yoshua Bengio, University of Montreal)